Fibonacci Sequence

Imagine you have a magical number garden. In this garden, each number is like a special seed, and it grows into a plant. Let’s start with the first two seeds: 0 and 1.

1. Planting the Seeds:
   • Plant the first seed, which is 0. This is the starting point.
   • Plant the second seed, which is 1. Now, we have two seeds in our garden.
2. Growing the Garden:
   • Each new plant in the garden is a special kind that grows from the sum of the two plants before it.
   • So, the third plant is 0 + 1 = 1.
   • The fourth plant is 1 + 1 = 2.
   • The fifth plant is 1 + 2 = 3.
   • The sixth plant is 2 + 3 = 5.
   • And it goes on: 8, 13, 21, 34, and so forth.
3. Counting Petals:
   • If you look closely at the flowers on these plants, you’ll notice something amazing. The number of petals on each flower follows the Fibonacci sequence!

Application – Counting Petals:

Now, let’s see an example of counting petals on flowers in our magical garden:

1. Flower 1 (First Plant): 0 petals
2. Flower 2 (Second Plant): 1 petal
3. Flower 3 (Third Plant): 1 petal
4. Flower 4 (Fourth Plant): 2 petals
5. Flower 5 (Fifth Plant): 3 petals
6. Flower 6 (Sixth Plant): 5 petals
7. Flower 7 (Seventh Plant): 8 petals
8. Flower 8 (Eighth Plant): 13 petals
9. And so on…

Real-Life Fun:

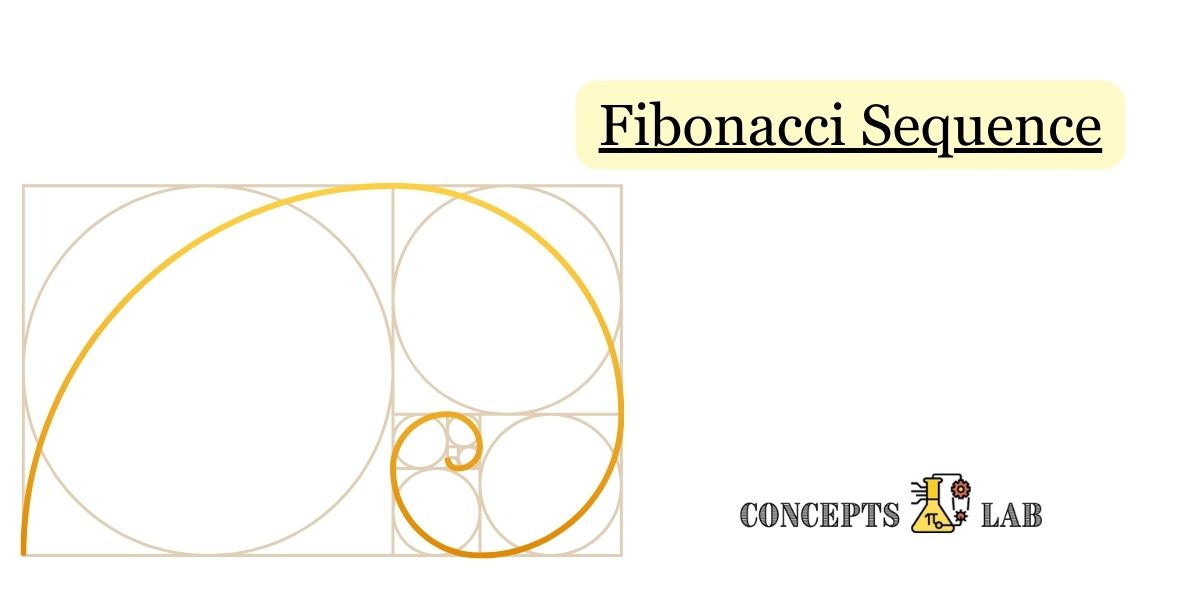
• Drawing Spirals: Connect the centers of the flowers with lines. You’ll notice beautiful spirals forming. These spirals follow the Fibonacci sequence, too!
• Sunflower Seeds: Count the spirals in the center of a sunflower, and you’ll likely find that the number of spirals follows the Fibonacci sequence.

The Fibonacci sequence, with its interesting mathematical properties, appears in various aspects of real life. Here are some applications of the Fibonacci sequence in different fields:

1. Nature and Biology:
   • Flower Petals: The number of petals in many flowers follows the Fibonacci sequence. For example, lilies have three petals, buttercups have five, and chicory has 21 petals.
   • Pinecones and Pineapples: The spirals in pinecones and pineapples often follow Fibonacci numbers.
   • Seed Heads: The arrangement of seeds in the center of a sunflower or a pinecone follows the Fibonacci sequence.
2. Art and Design:
   • Golden Ratio: The Fibonacci sequence is closely related to the golden ratio, which is often used in art and design to create aesthetically pleasing compositions. Artists and architects incorporate these ratios into their work for balance and harmony.
3. Finance and Stock Market:
   • Technical Analysis: Traders use Fibonacci retracement levels to identify potential levels of support and resistance in financial markets. The ratios derived from the Fibonacci sequence are believed to be significant in predicting price movements.
4. Computer Science:
   • Algorithms: Fibonacci numbers are used in computer algorithms, such as for searching and sorting data. They also appear in dynamic programming problems.
5. Mathematics and Number Theory:
   • Fibonacci Identity: The Fibonacci sequence has applications in number theory and algebra. There are several mathematical identities and properties associated with Fibonacci numbers.
6. Cryptography:
   • Random Number Generation: In certain cryptographic applications, Fibonacci sequences are used in the generation of pseudorandom numbers.
7. Phyllotaxis:
   • Leaf Arrangement: Phyllotaxis refers to the arrangement of leaves on a plant stem. The Fibonacci sequence is sometimes observed in the spiral patterns formed by leaves around the stem.
8. Human Body:
   • Body Proportions: Some proportions in the human body, such as the lengths of fingers, are said to approximate the golden ratio, which is related to the Fibonacci sequence.
9. Music:
   • Rhythmic Patterns: Musicians and composers sometimes use Fibonacci numbers to create interesting and rhythmic patterns in music.
10. Population Growth Models:
    • Idealized Population Growth: In idealized population growth models, the Fibonacci sequence can be used to represent the growth of a population over discrete generations.

These examples showcase how the Fibonacci sequence, with its unique mathematical properties, is not only a fascinating concept but also manifests in various aspects of the natural world and human endeavors.

Conclusion:

The Fibonacci sequence is like a magical pattern that appears in our number garden and even in the petals and spirals of flowers. It’s a fantastic way to see how math is connected to the wonders of nature!