The Seven Bridges of Königsberg

The Seven Bridges of Königsberg is a famous problem in the history of mathematics and graph theory. The problem is associated with the city of Königsberg (now Kaliningrad, Russia) and its seven bridges, which spanned the Pregel River and connected two large islands with the mainland. The problem was popularized by the Swiss mathematician Leonhard Euler in 1736.

The Problem:

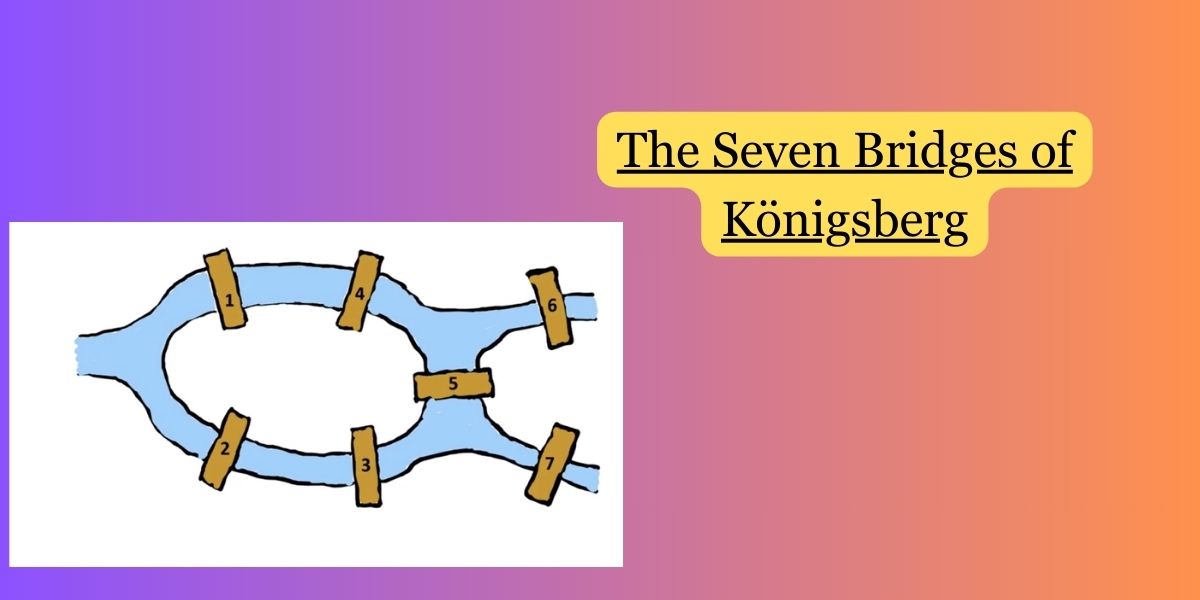
In Königsberg, there were two islands connected to each other and the mainland by seven bridges. The challenge was to find a walk through the city that would cross each bridge exactly once and return to the starting point.

Euler’s Solution:

Leonhard Euler approached the problem by abstracting it into a mathematical concept known as a graph. He represented the land masses as nodes and the bridges as edges connecting those nodes. Euler then asked a more fundamental question: Can you traverse each edge exactly once and return to the starting point?

Euler’s key insight was to recognize that for a walk to be possible, each node must have an even number of edges (except possibly for the starting and ending nodes). If a node has an odd number of edges, it is impossible to traverse each edge exactly once.

In the case of the Seven Bridges of Königsberg, each of the four land masses (nodes) was connected to an odd number of bridges. Since it was impossible to traverse each bridge exactly once with these conditions, Euler concluded that there was no solution to the problem.

Legacy:

Euler’s solution to the Seven Bridges of Königsberg problem laid the foundation for graph theory. His abstract approach not only solved a specific problem but also introduced a new way of thinking about networks and connectivity. Euler’s work in this area is considered a landmark in the development of modern mathematics.

The concept of Eulerian paths and circuits, as demonstrated in the Königsberg bridges problem, has applications in various fields, including computer science, transportation planning, and network analysis. Euler’s solution showcased the power of abstraction and the importance of considering the underlying structure of a problem.

While the citizens of Königsberg couldn’t take a stroll that crossed each bridge exactly once, Euler’s mathematical insights led to the creation of an entirely new branch of mathematics that continues to influence diverse areas of study today.